1.2 The Ideal Gas

For a low-density gas (atmospheric pressure and less), the equation:

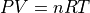
summarizes the relationships between these quantities:

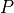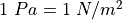• , the pressure of the gas. This is a force per unit area, as a Pascal A Newton (N) is 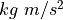so it is .

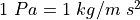  • You could notice that 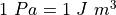, but I never did. We just stuck to standard units and trusted we didn’t get the math wrong.

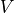• , the volume of the gas. This is measured in .

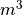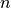• is the number of moles of the gas. A mole is Avogadro’s constant 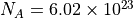particles, where each particle is a molecule of the gas.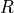

• is the constant 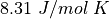A Joule (J) is a Newton-meter, so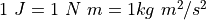

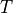• is the temperature in Kelvin .

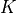Please be aware of some confusion!

Chemists like to use different units. * Pressure in atmospheres: 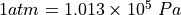(1 atmosphere

is the pressure at sea level, more or less.)

• Volume in liters.

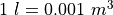
We often prefer working directly in the number of particles.

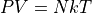
where:

• N is the number of particles, not moles.

• k is the Boltzmann Constant,

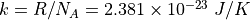
• Note that .

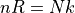When we first learned about the ideal gas law, our professor was careful to emphasize that it was only an approximation. We wondered why he was so emphatic that it was an approximation. The reason is because it works so well that you will start to trust it as if it is true, but it isn’t true for a wide variety of pressures and temperatures you will observe in the lab.

So while I emphasize that it is an approximation, let me also emphasize how well it works in practice! As long as you are in the right range, where the volume of the particles is much, much less than the volume of the gas, you can use this with remarkable accuracy.

We note the following predictions from the ideal gas law:

• .

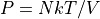  • If you hold the number of particles and temperature constant, and vary the volume, the pressure is inversely proportional. (Air Jordan’s work this way!)

  • If you hold the number of particles and the volume constant, and vary the temperature, the pressure is proportional. (This is how gas-pressure thermometers work.)

  • If you hold the pressure and temperature constant and vary the number of particles, the pressure is proportional. (IE, blowing up a balloon!)

• 

• 

• 

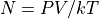
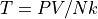
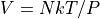
Note

It took me a while to realize this essential fact, and that is that it doesn’t matter what kind of molecules we’re talking about. If they are in gas phase, and their density is such that there is a lot of space between the molecules, then it will be the same temperature and pressure and volume as any other gas with the same number of particles.

This is pretty cool stuff. It has profound implications for chemistry, because it becomes rather simple to count the number of molecules in a gas: You just measure the volume, temperature and pressure and you know how many molecules are in the gas.

Problem Tips

1.9 and 1.10 are fairly standard algebra problems.

1.11 you need to understand what the implications of connecting the two rooms together. Even though both rooms can have different temperatures (there may be heat flowing from the warmer to the colder), the pressures will instantly find equilibrium. Note that even if the two rooms are at the same pressure and volume, that doesn’t mean they have the same temperature and number of molecules.

1.12 You can look up the size of these molecules online, or you can roughly estimate that they are about the wavelength of visible light.

1.13 Water is H2O obviously. The rule for calculating the mass of a mole of a substance is ridiculously easy, hence the unit.

1.14 A simple proportion problem.

1.15 Remember the for something to float, it must have the same density altogether as the stuff around it. To go up, it must be slightly less. To go down, slightly more. Where can we shed the 500 kg of mass needed in the hot-air balloon?

1.16 Probably the first problem to require at least a little knowledge of calculus. I won’t spoil this. It should probably be the hardest problem in the book so far. Estimating at least 10 minutes to solve, 30 if you’re rusty with calculus. Let me know if you need help, I can help figure out where you’re weak in math.

1.17 (DO THIS) The Virial Expansion! Brings back fond memories.

1. You probably want to see how far off the ideal gas law is from the virial expansion with 2 terms.

2. When he says, “think about the forces between molecules” keep in mind that they are tiny dipoles and quadrupoles. If you haven’t studied EM yet, then look up the Van Der Waals force. When molecules are too close, they are strongly repellant, but there is a “sweet spot” where they attract one another. If they go too far beyond that sweet spot they are repellant again. Further still and they are too far apart to either repel or attract.

3. The van der waals equation. Not much to say here. May take a while to work out the math. Should take less than an hour to solve. Pay attention to the trick. There is one other algebra trick that might take a while to solve. Just try to force the equation to look like the Virial Expansion.

4. Plotting a graph.

Part 2

This part tries to explain the ideal gas law using simple statistics and hand-waving.